数组和广义表的相关重要概念！！ - 数据结构 - 机器学习

1381 人阅读 | 时间：2021年01月15日 01:07

数组和广义表的相关重要概念！！ - 数据结构 - 机器学习 #daohang ul li t,.reed .riqi,a.shangg,a.xiatt,a.shangg:hover,a.xiatt:hover,a.shang,a.xiat,a.shang:hover,a.xiat:hover,.reed-pinglun-anniu,span.now-page,#daohangs-around,#caidan-tubiao,#daohangs,#daohangs li,#btnPost{background-color:#D10B04;} .dinglanyou1 h3{border-bottom:3px solid #D10B04;} #dibuer{border-top:2px solid #D10B04;}.cebianlan .rongqi h3{border-bottom:1px solid #D10B04;} #edtSearch{border:1px solid #D10B04;} #daohang .zuo ul li{border-right:1px solid #;} #daohang ul li t a{border-top:1px solid #;border-right:1px solid #D10B04;} #daohang ul li t a:hover{border-right:1px solid #;} #daohang .you ul li a:hover,#daohang .zuo ul li a:hover,.reed-pinglun-anniu:hover{background-color:#;} a:hover,.reed h6 a:hover,#dibuer a:hover,.reed .riqiding,.cebianlan .rongqi li a:hover,#pinglun-liebiao ul.fubens li.depth-1 dl dd span.shu a,#pinglun-liebiao ul.fubens li.depth-1 dl dd span.huifuliuyan a:hover,.reed-biaoti h6 span{color:#D10B04;} .reed .kan a{color:#0A0AF5;}.reed .kan a:hover{color:#D10101;} @media screen and (max-width:1492px){a.shang,a.xiat{background:none;} a.xiat:hover,a.shang:hover{background-color:#f9f9f9;background-image:none;text-decoration:none;}} var _hmt = _hmt || [];(function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?b19db5ba3b437a9e8698d2bc8fc64334"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s);})(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?b19db5ba3b437a9e8698d2bc8fc64334"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?2d748c9763cfc72fb7d1ccab29f0770d"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })(); var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = "https://hm.baidu.com/hm.js?f6d451f3f1be23f3abf240c64c469c1b"; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })();

数据结构 - 深度学习

当前位置：首页 » 数据结构精品文章 » 正文

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('

'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646162", container: s }); })();

数组和广义表的相关重要概念！！

1284 人参与 2018年09月03日 22:37 分类 : 数据结构精品文章评论

1、什么是数组，有哪些基本操作？

1）数组=(数据，顺序)。数组在程序设计中，为了处理方便，把具有相同类型的若干变量按有序的形式组织起来。这些按序排列的同类数据元素的集合称为数组。在Ｃ语言中，数组属于构造数据类型。一个数组可以分解为多个数组元素，这些数组元素可以是基本数据类型或是构造类型。因此按数组元素的类型不同，数组又可分为数值数组、字符数组、指针数组、结构数组等各种类别。

2）基本操作4个

(1) InitArray (＆A，n，bound1，…,boundn)建A 若维数n和各维长度合法，则构造相应的数组A，并返回OK

(2) DestroyArray(＆A)删A 销毁数组A

(3) Value(A，＆e，index1，…，indexn)取a A是n维数组，e为元素变量，随后是n个下标值。若各下标不超界，将e赋值为所指定的A的元素值，并返回OK

(4) Assign(＆A，e，index1，…，indexn)a←e赋值A是n维数组，e为元素变量，随后是n个下标值。若每个下标不超界，则将e的值赋给指定的A的元素，并返回OK

2、什么是稀疏矩阵，如何存储？

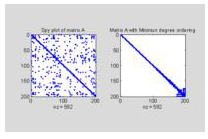
如果在矩阵中，多数的元素并没有数据，称此矩阵为稀疏矩阵（sparse matrix）。

矩阵在程序中常使用二维阵列表示，二维阵列的大小与使用的存储器空间成正比，如果多数的元素没有数据，则会造成存储器空间的浪费，为此，必须设计稀疏矩阵的阵列储存方式，利用较少的存储器空间储存完整的矩阵数据。

3、稀疏矩阵的优点。

稀疏矩阵的优点：稀疏矩阵的计算速度更快,因为M AT L A B只对非零元素进行操作,这是稀疏矩阵的一个突出的优点。假设矩阵A,B中的矩阵一样.计算2*A需要一百万次的浮点运算,而计算2*B只需要2 0 0 0次浮点运算。

对于一个用二维数组存储的稀疏矩阵Amn,如果假设存储每个数组元素需要L个字节,那么存储整个矩阵需要m*n*L个字节.但是,这些存储空间的大部分存放的是0元素,从而造成大量的空间浪费.为了节省存储空间,可以只存储其中的非0元素.

数组和广义表的相关重要概念！！ - 数据结构 - 机器学习

对于矩阵Amn的每个元素aij,知道其行号i和列号j就可以确定其位置.因此对于稀疏矩阵可以用一个结点来存储一个非0元素.该结点可以定义如下：[i,j,aij] 该结点由3个域组成,i:行号,j:列号;aij元素值.这样的结点被称为三元组结点。矩阵的每一个元素Qij,由一个三元组结点(i,j,aij)唯一确定。

4、数组使用中的几个注意点。

对于数组类型说明应注意以下几点：

1) 数组的类型实际上是指数组元素的取值类型。对于同一个数组，其所有元素的数据类型都是相同的。

2) 数组名的书写规则应符合标识符的书写规定。

3) 数组名不能与其它变量名相同，例如：

void main()

{ int a;

float a[10];

……

} 是错误的。

4) 方括号中常量表达式表示数组元素的个数，如a[5]表示数组a有5个元素。但是其下标从0开始计算。因此5个元素分别为a[0],a[1],a[2],a[3],a[4]。

5) 不能在方括号中用变量来表示元素的个数，但是可以是符号常数或常量表达式。例如：

#define FD 5

void main()

{ int a[3+2],b[7+FD];

……

} 是合法的。但是下述说明方式是错误的。

void main()

{ int n=5;

int a[n];

……

}

6) 允许在同一个类型说明中，说明多个数组和多个变量。

5、对数组赋值时需要注意什么？

Ｃ语言对数组的初始赋值还有以下几点规定：

1) 可以只给部分元素赋初值。当{ }中值的个数少于元素个数时，只给前面部分元素赋值。例如： static int a[10]={0,1,2,3,4};表示只给a[0]～a[4]5个元素赋值，而后5个元素自动赋0值。

2) 只能给元素逐个赋值，不能给数组整体赋值。例如给十个元素全部赋1值，只能写为： static int a[10]={1,1,1,1,1,1,1,1,1,1};而不能写为： static int a[10]=1;

3) 如不给可初始化的数组赋初值，则全部元素均为0值。

4) 如给全部元素赋值，则在数组说明中，可以不给出数组元素的个数。例如： static int a[5]={1,2,3,4,5};可写为： static int a[]={1,2,3,4,5};动态赋值可以在程序执行过程中，对数组作动态赋值。这时可用循环语句配合scanf函数逐个对数组元素赋值。

6、数组的降维存放示意图

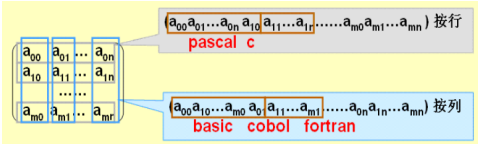
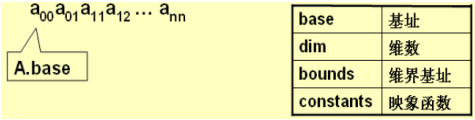
数组和广义表的相关重要概念！！ - 数据结构 - 机器学习

7、数组的定位公式

1维Loc(ai)=Loc(a1)+(i-1)×L 线性表的顺序存储

2维Loc(ai,j)=Loc(c1,c2)+[(b2-c2+1)×(i-C1)+(j-c2)]×L源于此式

=Loc(a0,0)+ [ (b2-c2+1)×i+j]×L简化后公式

Loc(i，j)=Loc(0，0)+ [ (b2+1)×i+j]×L

Loc(i，j)=Loc(0，0)+(b2×i+j)×L

元素个数（b1-c1+1）×（b2-c2+1）

来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=198

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('

'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646208", container: s }); })();

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('

'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646147", container: s }); })();

window._bd_share_config={"common":{"bdSnsKey":{},"bdText":"","bdMini":"2","bdPic":"","bdStyle":"0","bdSize":"16"},"share":{},"image":{"viewList":["qzone","tsina","tqq","renren","weixin"],"viewText":"分享到：","viewSize":"16"},"selectShare":{"bdContainerClass":null,"bdSelectMiniList":["qzone","tsina","tqq","renren","weixin"]}};with(document)0[(getElementsByTagName('head')[0]||body).appendChild(createElement('script')).src='http://bdimg.share.baidu.com/static/api/js/share.js?v=89860593.js?cdnversion='+~(-new Date()/36e5)];

数据结构

微信号：qq444848023 QQ号：444848023

加入【我是码农】QQ群：864689844（加群验证：我是码农）

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('

'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646186", container: s }); })();

(function() { var s = "_" + Math.random().toString(36).slice(2); document.write('

'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646175", container: s }); })();

搜索

数组和广义表的相关重要概念！！ - 数据结构 - 机器学习

数据结构 - 深度学习

数据结构 - 机器学习

当前位置：首页 » 数据结构精品文章 » 正文

数组和广义表的相关重要概念！！

1284 人参与 2018年09月03日 22:37 分类 : 数据结构精品文章评论

网站分类

标签列表

最近发表

评论专区

搜索

作者介绍

30天热门

热评文章

最近发表

标签列表

数组和广义表的相关重要概念！！ - 数据结构 - 机器学习

数据结构 - 深度学习

数据结构 - 机器学习

当前位置：首页 » 数据结构精品文章 » 正文

数组和广义表的相关重要概念！！

1284 人参与 2018年09月03日 22:37 分类 : 数据结构精品文章 评论

网站分类

标签列表

最近发表

评论专区

相关文章

搜索

作者介绍

30天热门

热评文章

最近发表

标签列表

1284 人参与 2018年09月03日 22:37 分类 : 数据结构精品文章评论